1. Kinematika hmotného bodu
Mechanika je základní obor fyziky, který se zabývá studiem pohybu a sil působících na tělesa. Její hlavní úlohou je pochopit a popsat, jak se objekty pohybují, jak na ně působí síly a jak tyto síly ovlivňují jejich pohyb.
Mechanika se dělí na tři hlavní oblasti:
- Kinematika: Popisuje pohyb těles bez zkoumání příčin tohoto pohybu, tedy bez ohledu na síly, které ho vyvolávají.
- Dynamika: Zkoumá pohyb těles v souvislosti se silami, které na ně působí. Vysvětluje, proč a jak se tělesa pohybují.
- Statika: Zabývá se tělesy v klidu nebo v rovnovážném stavu, kdy na ně působící síly jsou v rovnováze.
Mechanika je často považována za páteř klasické fyziky, protože poskytuje nástroje a zákony, jakou jsou newtonovy pohybové zákony, které popisují fungování nám důvěrně známeho světa. Její principy však sahají i do moderních věd, jako je kvantová mechanika a relativita, které rozšiřují její platnost do mikrosvěta a kosmu.
Obsah
Hmotný bod
Představte si, že jedete autem po dlouhé rovné silnici. Sledujete ubíhající krajinu, míjíte stromy a kolem vás sviští vzduch. Když ale potřebujete spočítat, jak daleko jste ujeli nebo jak dlouho vám cesta trvala, přemýšlíte o autě jako o celku, nebo jen o jednom bodě? Fyzika nám nabízí jednoduché řešení – myšlený hmotný bod, který usnadňuje výpočty a umožňuje nám pochopit pohyb těles. Pojďme si vysvětlit, co hmotný bod vlastně znamená a proč ho používáme.
Hmotný bod je myšlený bodový objekt, který má hmotnost, ale ale nemá žádné rozměry. V mechanice ho používáme pro zjednodušení analýzy pohybu, protože eliminuje nutnost zohledňovat složitější geometrické vlastnosti skutečných těles.
Hmotný bod nahrazuje těleso v případech, kdy jsou jeho rozměry zanedbatelné ve srovnání s uvažovanými vzdálenostmi pohybu. Typickým příkladem je studium planet na oběžné dráze nebo automobilů pohybujících se po dlouhé silnici, kde velikost objektů nehraje roli.
Hmotný bod se umysťuje do těžiště tělesa, což je bod, kde se zdá, že je soustředěna celková hmotnost tělesa a umisťujeme do něj všechny síly působící na těleso (viz. 3. kapitola). Toto zjednodušení umožňuje soustředit se na kinematické vlastnosti pohybu a vyhnout se komplikacím spojeným s nerovnoměrnou distribucí hmoty v tělese nebo jeho rotací.

Reklamní slogan:
Hmotný bod – když na velikosti nezáleží, ale na pohybu ano!
Hmotný bod je tedy myšlený bodový objekt, který nemá rozměry, respektive jeho rozměry jsou zanedbatelné ve srovnání s uvažovanými vzdálenostmi. Toto zjednodušení nám umožňuje analyzovat pohyb a síly bez komplikací spojených s tvarem a velikostí objektu. Nyní se pojďme podívat na příklady hmotných bodů a vysvětlení, proč je můžeme považovat za hmotné body.
Příklad hmotného bodu:
- Pohyby planet po oběžných drahách: Při výpočtech oběžných drah planet zjednodušujeme reálné objekty na hmotné body, jelikož rozměry planet jsou zanedbatelné vůči vzdálenostem v kosmu.
- Vzdálenost mezi Sluncem a Merkurem je natolik velká, že velikost samotných těles nemá významný vliv na pohyb.
- Příkladme může být planeta Merkur a vzdálenost od Slunce. Merkur má průměr 4879 km. Průměrná vzdálenost mezi Merkurem a Sluncem je 57 900 000 km, přičemž Merkur na této vzdálenosti představuje pouze 0.000085%. To jistě uznáte, že je zanedbatelné procento, které nám při výpočtech nezpůsobí žádnou závažnou chybu.
- Jiný příklad je planeta Země a její oběžná dráha. Průměr Zěme je 12 756 km a její oběžná dráha má délku 940 000 000 km. Poloměr Země na její oběžné dráze představuje jen asi 0.000014%. Což je podbně zanedbatelné číslo jako v případě Merkuru a jeho vzdálensoti od Slunce.
- Auto jedoucí po dlouhé silnci: Při výpočtech pohybu aut po dlouhých silnicích zjednodušujeme reálné objekty na hmotné body, protože rozměry aut jsou zanedbatelné ve srovnání s délkou trasy, kterou urazí.
- Například u běžného osobního auta, které má délku přibližně 4,5 metru, je tento rozměr nesrovnatelný s délkou silnice. Pokud auto jede po dálnici dlouhé 100 kilometrů (100 000 metrů), délka auta představuje pouhých 0,0045% této vzdálenosti. Toto zanedbatelné procento nijak neovlivní výpočty spojené s časem a vzdáleností.
Ještě výraznější je to u delších tras. Pokud by například auto jelo trasu dlouhou 1000 kilometrů (1 000 000 metrů), délka auta by tvořila už jen 0,00045% této vzdálenosti. To je zanedbatelný rozdíl, který nám umožňuje považovat auto za hmotný bod bez výrazného zkreslení výsledků.
- Naopak o něco méně výrazný rozdíl je u kratších vzdáleností. Pokud by auto jelo trasu dlouhou 1 kilometr (1 000 metrů), délka auta by představovala 0,45% této vzdálenosti. I když je toto procento vyšší než u delších tras, stále je dostatečně malé na to, aby bylo možné auto považovat za hmotný bod.
- I když by auto urazilo vzdálenost pouhých 100 metrů, stále jej můžeme považovat za hmotný bod. V tomto případě délka auta představuje 4,5 % vzdálenosti, což je sice výrazně více než u delších tras, ale při pohybu vpřed se rozměry auta neprojeví natolik zásadně, aby ovlivnily výsledky výpočtů. Často nás totiž zajímá především celková uražená vzdálenost nebo čas, který auto na této trase strávilo. V takových případech lze hmotný bod umístit například na kapotu auta, aniž by tím byla ztracena obecnost výpočtů. Tento přístup umožňuje snadno určit čas, kdy kapota auta opustila startovní čáru, a kdy naopak projela cílovou páskou.
- Mnoho dalšího…
Na druhou stranu existují situace, kdy hmotný bod není vhodným zjednodušením. V těchto případech rozměry, tvar nebo rozložení hmotnosti objektu hrají klíčovou roli, a jejich zanedbání by vedlo k nepřesným výsledkům nebo chybnému závěru. Pojďme se nyní podívat na příklady, kdy hmotný bod nepostačuje, a vysvětleme si, proč je nutné brát v úvahu celý objekt.
Co není hmotný bod:
- Parkování auta: Rozměry auta jsou zde zásadní, protože se auto musí vlézt do parkovacího prostoru. Tvar a velikost hrají klíčovou roli při manévrování a určování, zda auto zaparkuje správně.
- Loď proplouvající úzkým průplavem: Velikost a šířka lodi jsou klíčové, protože loď musí přesně manévrovat v omezeném prostoru a její rozměry nelze zanedbat.
Most a nákladní auto: Pokud na most vjede těžké nákladní auto, jeho rozložení hmotnosti může být zásadní. Rozměry auta rozhodují o tom, kde se hmotnost koncentruje a jak ovlivní stabilitu mostu.
Vlak na železničním mostě: Délka vlaku může být klíčová, protože je třeba zohlednit, zda most unese celkovou hmotnost vlaku rovnoměrně rozloženou po celé délce.
- Stůl na nerovném povrchu: Pokud řešíme stabilitu stolu na nerovné zemi, je nutné brát v úvahu délku a rozmístění jeho nohou, aby bylo možné zjistit, zda je stabilní.
- Pohyblivé rameno jeřábu: Délka ramena a jeho rozměry jsou klíčové při zvedání břemen. Nelze jeřáb zjednodušit na bod, protože stabilita a nosnost závisí na celé konstrukci.
- Let balónu při větrných podmínkách: Velikost a tvar balónu ovlivňují jeho pohyb a způsob, jakým ho ovlivňuje vítr. Rozměry jsou zásadní pro pochopení jeho aerodynamiky.
- Křídlo letadla ve větrném tunelu: Aerodynamika křídla závisí na jeho přesném tvaru, což je klíčové pro pochopení vztlaku a odporu.
- Raketa startující z rampy: Tvar a velikost rakety ovlivňují její aerodynamiku, spotřebu paliva a trajektorii, což jsou klíčové faktory při jejím pohybu.
- Částice v mikroskopu: Pokud sledujeme částici pod mikroskopem, její rozměry a struktura mají zásadní vliv na její pohyb a interakce s okolím. (viz. Brownův pohyb)
- Rotující planeta: Pokud analyzujeme rotaci planety, je nutné zohlednit její tvar (například zploštění na pólech), což ovlivňuje její gravitační pole a pohyb.
- Mnoho dalšího…
Určitě jste si všimli, že některé příklady a protipříklady se vzájemně překrývají. To není náhoda – v určitých situacích může být těleso zjednodušeno (aproximováno) jako hmotný bod, zatímco jindy je to nevhodné a je nutné zohlednit jeho rozměry, tvar nebo rozložení hmotnosti. Vše záleží na kontextu a na tom, jaké aspekty pohybu či sil nás zajímají. Pojďme se tedy podívat blíže na tyto sporné situace a vysvětlit si, co rozhoduje o tom, zda můžeme těleso považovat za hmotný bod, nebo nikoliv.
Sporné příklady hmotného bodu:
- Loď na moři:
- Hmotný bod: Při plavbě na otevřeném moři, kde vzdálenosti dosahují stovek kilometrů, může být loď zjednodušena na bod.
- Není hmotný bod: Při průjezdu úzkým kanálem (například Suezským průplavem) záleží na tvaru a šířce lodě, stejně tak na šířce a tvaru kanálu, ktreré jsou důležité aby se zabránilo kolizi.
- Cyklista na závodní dráze:
- Hmotný bod: Pokud analyzujeme celkovou vzdálenost a čas závodu, můžeme cyklistu považovat za bod.
- Není hmotný bod: Pokud se soustředíme na aerodynamiku cyklisty, rozložení jeho těla a odpor vzduchu, jeho tvar a velikost hrají zásadní roli.
- Padající míč:
- Hmotný bod: Pokud nás zajímá jen doba pádu a výška, lze zanedbat tvar a velikost míče.
- Není hmotný bod: Pokud míč rotuje nebo je vystaven odporu vzduchu, jeho tvar a velikost ovlivňují trajektorii.
- Měsíc obíhající Zemi:
- Hmotný bod: Pokud se zabýváme oběžnou dráhou, můžeme zanedbat velikost Měsíce.
- Není hmotný bod: Při výpočtech přílivu a odlivu na Zemi je třeba vzít v úvahu jeho rozložení hmoty a tvar.
- Planetka blížící se k Zemi:
- Hmotný bod: Pokud nás zajímá pouze její trajektorie a rychlost.
- Není hmotný bod: Pokud analyzujeme, jaký kráter vytvoří při dopadu, je nutné zohlednit její velikost a tvar.
- Elektron obíhající jádro atomu:
- Hmotný bod: V klasickém modelu atomu, kde zanedbáváme jeho vlnové vlastnosti.
- Není hmotný bod: V kvantové mechanice, kde se elektron chová jako vlna a má pravděpodobnostní rozložení.
- Mnoho dalšího…
Shrnutí
Hmotný bod nám ukazuje, že i složité objekty lze v mnoha situacích zjednodušit na pouhý bod, aniž bychom přišli o podstatu jejich pohybu. Tento koncept nám umožňuje pochopit a popsat svět kolem nás s překvapivou elegancí a přesností. Klíčem však je vždy zvážit, kdy je takové zjednodušení vhodné. A právě tady se fyzikové často ptají: „Mohu to těleso opravdu považovat za hmotný bod?“
Relativita klidu a pohybu
Představte si, že sedíte na lavičce v parku. Kolem vás prochází lidé, míjí vás auta a nad vámi možná proletí pták. Zdá se vám, že sedíte v klidu, ale jste opravdu v klidu? Fyzika nám říká, že odpověď není tak jednoduchá. Pojďme si to společně vysvětlit.

Klid a pohyb záleží na tom, k čemu se vztahuje:
- Těleso je v klidu vůči jinému tělesu, pokud vzhledem k němu nemění svou polohu. Když sedíte na lavičce, jste v klidu vůči lavičce – vaše poloha vůči ní se nemění. Ale co když se podíváte na auto, které projíždí kolem? Vůči autu jste v pohybu, protože vaše poloha vzhledem k autu se mění.
- Těleso je v pohybu vůči jinému tělesu, pokud vzhledem k němu mění svou polohu. Auto projíždějící parkem je vůči lavičce v pohybu, protože jeho poloha se vůči lavičce mění. Ale co lidé sedící v autě? Ti jsou vůči autu v klidu, protože jejich poloha vůči sedadlu se nemění.
Vztažná soustava: Klíč k pochopení pohybu
Pohyb nebo klid těles nikdy nelze určit jednoznačně. Abychom mohli říct, zda je těleso v klidu nebo v pohybu, potřebujeme vždy určit tzv. vztažné těleso (nebo vztažnou soustavu). Vztažné těleso je objekt, ke kterému vztahujeme pohyb nebo klid jiného tělesa.
Příklad vztažné soustavy:
- Když sedíte na lavičce, vztažné těleso může být lavička (vůči které jste v klid) nebo jedoucí auto (vůči kterému se pohybujete).
- Pokud sledujete z lavičky Měsíc na obloze, můžete říct, že je v pohybu vůči Zemi, ale zároveň Země je vůči vám v klidu.
Klid je relativní, absolutní klid neexistuje
A teď se dostáváme k jedné z fascinujících myšlenek fyziky: klid je relativní. To znamená, že klid vždy závisí na tom, k čemu jej vztahujeme. Neexistuje žádný „absolutní klid“ ve vesmíru, protože všechna tělesa se neustále pohybují vzhledem k jiným tělesům.
Příklad pohynu planety Země:
- Země se točí kolem své osy a zároveň obíhá kolem Slunce.
- Slunce obíhá kolem středu naší galaxie.
- A naše galaxie se pohybuje vesmírem.
Jak je vidět vždy najdeme jiné těleso vůči kterému se planeta Země pohybuje -> něco jako absolutní klid neexistuje.
Reklamní slogan:
Relativita v akci: Když všechno stojí, ale všechno se zároveň pohybuje.
Shrnutí:
Relativita klidu a pohybu nám ukazuje, že nic není tak pevně dané, jak by se mohlo zdát. Vždy záleží na tom, vůči čemu klid nebo pohyb posuzujeme. A právě tohle je klíčem k pochopení mnoha dalších fyzikálních principů. Teď už víte, proč si fyzikové nikdy neodpustí otázku: „Vzhledem k čemu?“
Zajímavost – Nejrychlejší auto na světe:
Na okraji pouště Mojave (Kalifornie v USA) se připravovalo nejrychlejší auto světa, Sonic Blazer, k pokusu o překonání rychlostního rekordu. Toto technické mistrovské dílo dokázalo dosáhnout rychlosti až 1600 km/h – rychleji než většina letadel.
Ale jak rychlé vlastně Sonic Blazer je? Záleží na tom, koho se ptáte – nebo spíš, z jaké vztažné soustavy se na to díváte.
- Mechanici, kteří sledovali Sonic Blazer z pevně ukotveného stanoviště na zemi, viděli auto jako šmouhu, která proletěla rychlostí 1600 km/h. Vzhledem k jejich vztažné soustavě, která byla spojena s povrchem Země, se auto pohybovalo touto závratnou rychlostí. Z jejich pohledu se oni sami nehýbali – pouze auto „letělo“ po dráze.
Řidič Sonic Blazeru měl na věc úplně jiný pohled. V kabině auta se necítil, že by letěl rychlostí 1600 km/h. V jeho vztažné soustavě byl v klidu, protože jeho poloha vzhledem k volantu, sedačce nebo pedálům se vůbec neměnila. Pro něj byl v pohybu spíše celý svět kolem.
- Na oběžné dráze sledoval pokus satelit. Z jeho pohledu se Sonic Blazer nejen pohyboval rychlostí 1600 km/h po poušti, ale také s ním uháněla celá Země. Planeta se točila kolem své osy rychlostí přibližně 1670 km/h. Vůči satelitu se auto mohl pohybovat klidně až 3270 km/h nebo i více (v závislosti na směru auta vůři rotaci Země a směru a ryclosti pohybu satelitu).
- Z pohledu Slunce byla situace ještě zajímavější. Sonic Blazer, Země, Měsíc a všechny planety Sluneční soustavy se pohybovaly společně Galaxií rychlostí 828 000 km/h. Rychlost auta byla v této vztažné soustavě zcela zanedbatelná – jako když pozorujete mravence pohybujícího se na povrchu vlaku, který uhání krajinou.
Rychlost auto Sonic Blazer tedy vždy záleží na soustavě vůči které pohyb pozorujeme.
Trajektorie vs. Dráha
Představte si, že sledujete ptáka letícího po obloze. Pták během svého letu vykresluje ve vzduchu neviditelnou křivku – to je trajektorie. Trajektorie je geometrická křivka, která popisuje pohyb hmotného bodu. Trajektorie nám říká, kudy se bod pohybuje, ale neříká nic o tom, jak dlouhou vzdálenost při tom urazil.
Dráha naopak není o tvaru pohybu, ale o jeho délce. Dráha je celková vzdálenost, kterou hmotný bod při svém pohybu podél trajektorie urazí. Jinými slovy, zatímco trajektorie je křivka, kterou bod sleduje, dráha je délka této křivky.
Příklad trajektorie vs. Dráha:
- Pokud se auto pohybuje po rovné silnici, trajektorie je přímka a dráha odpovídá její délce.
- Pokud ale jede po klikaté horské cestě, trajektorie bude zakřivená a dráha bude delší než vzdálenost mezi počátečním a koncovým bodem.
Trajektorie a dráha spolu úzce souvisí, ale každá z nich vyjadřuje jinou vlastnost pohybu.
Jednotky dráhy:
Jednotkou dráhy v soustavě SI je metr (\(\text{m}\)), který představuje základní délkovou jednotku. V praxi se však často setkáváme i s jinými jednotkami, jako jsou kilometry (\(\text{km}\)) pro větší vzdálenosti nebo centimetry (\(\text{cm}\)) a milimetry (\(\text{mm}\)) pro menší délky. Ale existují i jiné jednotky, některé pocházejí z historie jako loket, jiné se používají méně jako decimetr. Při převodech platí, že \( 1\,\text{km} = 1000\,\text{m}, \text{ } 1\,\text{m} = 100\,\text{cm} \text{ a } 1\,\text{cm} = 10\,\text{mm} \)..
Reklamní slogan:
Cesta má tvar – to je trajektorie. Cesta má délku – to je dráha.
Rychlost
Představte si, že jedete autem po dálnici. Tachometr vám ukazuje rychlost, ale co to vlastně znamená? Vědecky řečeno, rychlost je vektorová veličina, což znamená, že má nejen velikost (jak rychle jedete), ale také směr (kam jedete). Jinými slovy, rychlost udává, jak se mění poloha hmotného bodu v čase. Rychlosti se někdy říká i dráhová rychlost jelikož označuje změnu dráhy za jednotku času. (více o vektorových veličinách se dočtete zde)

Jak je to s těmi vektorovými veličinami:
Vektorové veličiny jsou základním stavebním kamenem fyziky. Na rozdíl od skalárních veličin, které jsou určeny pouze svou velikostí (například hmotnost nebo teplota), mají vektorové veličiny kromě velikosti také směr. To znamená, že nám poskytují mnohem více informací o pohybu, síle nebo jiných fyzikálních jevech, které popisují.
Při práci s vektory používáme specifické značení, které nám pomáhá jasně rozlišit mezi vektorem samotným a jeho velikostí. Pokud mluvíme o vektoru, označujeme ho šipkou nad symbolem, například \(\vec{v}\) (vektor rychlosti). Když ale chceme hovořit pouze o velikosti tohoto vektoru, šipku vynecháme, například \(v\) (velikost síly). Velikost vektoru taky můžeme označit následovně: \(\|\vec{v}\|\). Toto rozlišení je klíčové pro správné pochopení fyzikálních rovnic a konceptů.
Kdybyste nad vektory tápali můžete si o nich přečíst tento článek!!!
Jednotky rychlosti:
Základní jednotka rychlosti je metr za sekundu \(\text{m/s}\). Například pokud auto urazí 10 metrů za 1 sekundu, jeho rychlost je 10 \(\text{m/s}\). V každodenním životě ale častěji používáme kilometry za hodinu \(\text{km/h}\), což odpovídá 3,6krát větší hodnotě. Níže je jak převádíme metry za sekundu na kilometry za hodinu včetně vysvětlení proč násobíme právě 3,6x.
Ukázka převodu jdenotek u rychlosti:
Základní jednotka rychlosti je:
\(1 \text{ m/s}\)
Metr je \(\frac{1}{1000}\) kilometru a hodina je \(\frac{1}{60}\) minuty což je \(\frac{1}{3600}\) sekundy, tedy dostavame:
\(1 \text{ m/s} = 1 \frac{\frac{1}{1000} \text{ km}}{\frac{1}{3600} \text{ h}}\)
Po základních matematických úpravách se složenými zlomky dostáváme:
\(1 \text{ m/s} = 1 \frac{3600 \text{ km}}{1000\text{ h}}\)
Když výraz upravíme dostáváme:
\(1 \text{ m/s} = 3,6 \text{ km/h}\)
Obrácený převod podle pravidel matematiky je:
\(\frac{1}{3,6}\text{m/s} = 1 \text{ km/h}\)
Typy rychlosti: více než jen číslo na tachometru
Rychlost není jen údaj, který nám poskytuje přehled o tom, jak rychle se pohybujeme. Je to jeden z nejdůležitějších nástrojů fyziky, který nám pomáhá popsat pohyb těles, analyzovat situace v reálném světě a modelovat složité jevy. V každodenním životě ji vnímáme jako číslo na tachometru, ale v kontextu fyziky je rychlost mnohem hlubší pojem. Pojďme se podívat, jaké základní typy rychlosti rozlišujeme a co nám říkají o světě kolem nás.
Rychlost rozlišujeme na dvě základní složky:
- Okamžitá rychlost: Velikost rychlosti v konkrétním bodě na trajektorii a v daném okamžiku. Představte si ji jako to, co ukazuje tachometr právě teď. Matematicky ji definujeme jako průměrnou rychlost na velmi malém úseku dráhy a v krátkém časovém intervalu. Vzorec:
\(\vec{v}=\frac{\Delta\vec{s}}{\Delta t}\), kde \(\Delta t \rightarrow 0\)
\(\vec{v}\) – vektor okamžité rychlosti \([\text{m/s}]\)
\(\Delta\vec{s}\) – změna dráhy \([\text{m}]\)
\(\Delta t\) – časový interval (změna času), který jde k 0 sekundám \([\text{s}]\)
- Průměrná rychlost: Vypočítáme ji jako podíl celkové dráhy a času potřebného k jejímu překonání. Říká nám, jaká by byla stálá rychlost, pokud bychom celou dobu jeli stejnou rychlostí. Tato rychlost se dá vyjádřit jako vektrová veličina ale mnohem častěji se vyjadřuej jako sklární, proto v následujícím vzorci chybí typická šipka pro vektor. Vzorec:
\(v=\frac{s}{t}\)
\(v\) – průměrná rychlost \([\text{m/s}]\)
\(s\) – dráha, kterou hmotný bod urazil \([\text{m}]\)
\(t\) – čas, za který hmotný bod urazil dráhu \(s\) \([\text{s}]\)
Shrnutí:
Rychlost tedy není jen vektor – je to klíč k pochopení pohybu, směru a času. V každém okamžiku nám říká, jak rychle a kam se pohybujeme, a pomáhá nám analyzovat a modelovat pohyb těles v reálném světě.
Zrychlení
\(\vec{a}=\frac{\Delta\vec{v}}{\Delta t}\)
\(\vec{a}\) – vektor zrychlení \([\text{m/s}^2]\)
\(\Delta \vec{v}\) – změna vektoru rychlosti \([\text{m/s}]\)
\(\Delta t\) – časový interval (změna času) \([\text{s}]\)
Jednotky zrychlení:
Zrychlení se nejčastěji měří v metrech za sekundu na druhou \(\text{m/s}^2\), které jsou zároveň základní jednotkou. Pokud je zrychlení 1 \(\text{m/s}^2\), znamená to, že rychlost tělsa se každou sekundu změní o 1 \(\text{m/s}\). Jiné použivané jednotky jsou například kilometry za hodinu na druhou \(\text{km/h}^2\).
Směr zrychlení: Co nám říká o pohybu?
Zrychlení je vektorová veličina (tedy má velikost i směr), která nejen popisuje změnu rychlosti, ale také odhaluje, co se s pohybem tělesa skutečně děje. Směr zrychlení je zásadní pro pochopení toho, zda těleso svou rychlost zvětšuje, zmenšuje nebo mění směr pohybu. Představme si auto – v jednom okamžiku přidává plyn, jindy brzdí, a někdy dokonce zatáčí. To vše souvisí se zrychlením.
- Zrychlení je kladné, respektive jeho směr je stejný jako směr rychlosti: Hmotný bod se pohybuje stále rychleji (např. auto, které přidává plyn).

- Zrychlení je záporné, respektive jeho směr je opačný ke směru rychlosti: Hmotný bod zpomaluje (např. auto, které brzdí). Toto záporné zrychlení se často označuje jako zpomalování.

Směr zrychlení tak odhaluje nejen to, zda pohyb pokračuje stejným tempem, ale i to, jakým způsobem se mění.
Složky zrychlení: Tečné a normálové
- Tečné zrychlení (\(\vec{a_t}\)): Odpovídá změně velikosti rychlosti (např. zrychlování při přidávání plynu).
- Normálové zrychlení (\(\vec{a_n}\)): Odpovídá změně směru pohybu (např. při zatáčení auta).
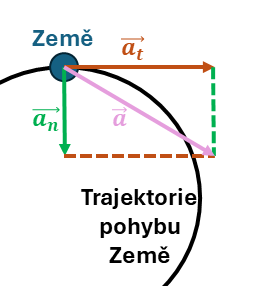
Proč je zrychlení důležité?
Zrychlení je klíčovým pojmem v kinematice, protože nám pomáhá pochopit, jak se pohyb hmotného bodu (případně tělesa) mění v závislosti na čase. Díky zrychlení můžeme popsat nejen pohyb rovnoměrný, ale i složitější pohyby, jako je zrychlování, zpomalování nebo pohyb po zakřivené dráze. Bez něj bychom jen těžko porozuměli tomu, jak se mění rychlost auta, proč padá jablko stále rychleji, nebo jak kosmické lodě dosahují své oběžné dráhy.
Rozdělení pohybů
Pohyb je základním projevem hmotných těles a každý z nás se s ním setkává každý den, ať už jde o chůzi, jízdu na kole nebo pohyb planet na obloze. Ale věděli jste, že pohyby lze rozdělit do několika kategorií podle jejich různých charakteristik? Způsob, jakým těleso cestuje prostorem, tvar trajektorie, po které se pohybuje, nebo změna rychlosti během pohybu – to všechno jsou aspekty, které fyzikové zkoumají a podle nichž pohyby třídí. Pochopení těchto rozdílů nám umožňuje lépe popsat a analyzovat pohyb v reálném světě, od nejjednodušších každodenních situací až po složité jevy v přírodě. Pojďme se na to podívat podrobněji!
Podle způsobu pohybu tělesa:
- Trajektorie: Přímka nebo libovolná křivka.

Příklad posuvného pohybu:
- Auto jedoucí po rovné silnici
- Výtah pohybující se mezi patry
- Vlak na rovných kolejích
- Pohyb stolu po hladké podlaze
- Sáně klouzající po sněhu
- Lodní kontejner na přepravníku
- Pás na eskalátoru
- Mnoho dalšího…
2. Otáčivý pohyb: Každý bod tělesa opisuje kružnici (nebo její část), přičemž všechny kružnice mají společný střed na jedné přímce – ta se nazývá osa otáčení.
Pozor při tomto druhu pohybu nemůžeme zaměnit těleso za hmotný bod.
- Trajektorie: Kružnice a nebo její část (jednotlivých bodů tvořící těleso).

Příklad otáčivého pohybu:
- Kolo u auta (jeho rotační pohyb)
- Ručky hodin
- Země rotující kolem své osy
- Gramofonová deska
- Pohyb bubnu pračky
- Vrtule letadla
- Disk u cirkulárky
- Otáčení kliky u dveří
- Víčko lahve při zavírání nebo otevírání
- Mnoho dalšího…
Podle tvaru trajektorie:
Pohyb tělesa můžeme také rozlišit podle tvaru trajektorie, kterou těleso při svém pohybu opisuje. Někdy se jedná o přímočarý pohyb, jako když padají kapky deště, jindy o křivočarý pohyb, který sledujeme třeba u míče při kopu na bránu. Tvar trajektorie nám pomáhá lépe porozumět povaze pohybu a popsat jej přesněji. Pojďme se podívat, jak se tyto trajektorie liší a kde je můžeme v reálném světě pozorovat.
1. Přímočarý pohyb: Těleso se pohybuje po přímce.

Příklad přímočarého pohybu:
- Auto jedoucí po rovné silnici
- Padající míč
- Výtah pohybující se nahoru nebo dolů mezi patry
- Běžec sprintující na rovné dráze
- Vlak jedoucí po přímém úseku kolejí
- Pohyb zásuvky při otevírání a zavírání
- Mnoho dalšího…
2. Křivočarý pohyb: Těleso se pohybuje po křivce.

Příklad křivočarého pohybu:
- Auto zatáčející na kruhovém objezdu
- Planeta obíhající kolem Slunce
- Let letadla během klesání v zatáčce
- Houpání houpačky na dětském hřišti
- Pohyb auta po horských serpentinách
- Pád papíru (křivočarý díky vzdušnému odporu)
- Satelit obíhající kolem Země
- Mnoho dalšího…
1. Rovnoměrný pohyb: Těleso urazí za stejné časové úseky vždy stejné dráhy.

Příklad rovnoměrného pohybu:
- Vlak jedoucí po přímé trati konstantní rychlostí
- Automatický dopravník v továrně posouvající zboží rovnoměrně
- Lidé stojící na eskalátoru
- Běžec na běžícím pásu
- Auto jedoucí po dálnici za pomoci tempomatu
- Loď plující vodě konstantní rychlostí
- Mnoho dalšího…
2. Nerovnoměrný pohyb: Těleso urazí za stejné časové úseky různé dráhy. Nerovnoměrný pohyb dělíme na:
- Zrychlený pohyb: Těleso se pohybuje stále rychleji.

Příklad zrychleného pohybu:
- Letadlo při vzletu na ranveji
- Běžec zrychlující při startu závodu
- Zrychlující vlak opouštějící stanici
- Padající jablko
- Lyžař sjíždějící prudký svah
- Sportovní auto akcelerující na závodní dráze
- Skokan na lyžích při jízdě po nájezdové rampě
- Vozík na horské dráze zrychlující ve sjezdu
- Motorka na závodní dráze při akceleraci na rovince
- Mnoho dalšího…
- Zpomalený pohyb: Těleso zpomaluje.

Příklad zpomaleného pohybu:
- Letadlo při přistávání
- Auto zpomalující před semaforem
- Lyžař brzdící plužením na svahu
- Motorka snižující rychlost před zatáčkou
- Parašutista po otevření padáku
- Kámen vržený vzhůru
- Vlak přibližující se ke stanici
- Mnoho dalšího…
Při zrychleném nebo zpomaleném pohybu nemusí vždy platit, že změna rychlosti probíhá plynule a pravidelně. Proto rozlišujeme dva typy:
Rovnoměrně zrychlený pohyb – Rychlost tělesa se zvětšuje stále stejným způsobem, tedy za každou sekundu přibývá stejný přírůstek rychlosti. Jinými slovy zrychlení je konstantí v čase.
Nerovnoměrně zrychlený pohyb – Zde se rychlost mění nepravidelně, tedy přírůstky rychlosti nejsou konstantní. Jinými slovy zrychlení je proměné v čase.
Rovnoměrně zpomalený pohyb – Rychlost klesá stále stejným tempem. Zrychlení v čase je konstantí.
Nerovnoměrně zpomalený pohyb – Rychlost klesá nepravidelně. Zrychlení v čase je nepravidelné.
Toto rozlišení nám pomáhá lépe pochopit různé situace v reálném světě, kde pohyby nemusí být vždy ideální a dokonale rovnoměrné.
Proč je důležité pohyby rozlišovat?
Pohyb rovnoměrný
Představte si, že jedete po dálnici se zapnutým tempomatem. Rychlost vašeho auta zůstává stále stejná – nebrzdíte, nezrychlujete, jen rovnoměrně ukrajujete kilometry. Přesně takový pohyb označujeme jako rovnoměrný pohyb. Jinak řečeno: Pohyb je rovnoměrný, pokud těleso urazí za stejné časové úseky stejnou dráhu. To znamená, že rychlost tělesa se během pohybu nemění.
Matematicky ho můžeme popsat jednoduchými vztahy:
Rychlost je konstantní:
Dráha \(s\) se mění lineárně s časem:
\(s=s_{0}+v\times t\)
\(s\) je celkem uražená dráha [\(\text{m}\)]
\(s_{0}\) je počáteční dráha (např. místo, kde auto vyjelo, ale rychlost na této dráze neznáme) [\(\text{m}\)]
\(v\) je konstantní rychlost [\(\text{m/s}\)]
\(t\) je uplynulý čas, po který jsme se pohybovali rychlostí \(v\) [\(\text{s}\)]
Tento vztah nám říká, že dráha lineárně roste s časem, což můžeme vidět i na grafu závislosti dráhy na čase – je to přímka se směrnicí (strmostí) odpovídající rychlosti pohybu.
Rovnoměrný pohyb je ideální model, který v přírodě téměř neexistuje, protože většina pohybů je ovlivněna brzděním, zrychlováním nebo odporem prostředí. Přesto se používá jako základní stavební kámen pro složitější pohyby.
Simulátor rovnoměrného pohybu
Vizualizujte, jak se pohyb mění v čase!
Co můžete dělat?
- Nastavte počáteční polohu – vyberte, kde těleso začíná (metry, kilometry…).
- Zvolte rychlost pohybu – experimentujte s různými jednotkami (m/s, km/h…).
- Upravte délku simulace – zvolte maximální čas (sekundy, minuty, hodiny).
- Spusťte simulaci – sledujte, jak se těleso pohybuje v čase!
- Pauzněte a resetujte – zastavte simulaci, nebo začněte znovu.
- Uložte si graf – stáhněte vizualizaci jako obrázek pro další analýzu.
Jak to funguje?
Tento simulátor vizualizuje rovnoměrný pohyb – tedy pohyb, při kterém těleso urazí za stejné časové úseky stejnou dráhu. Graf zobrazuje dráhu \(s=s_{0}+v\times t\), kde můžete sledovat aktuální polohu v čase.
Vyzkoušejte různé scénáře – co se stane, když zvýšíte rychlost? Jaký vliv má změna jednotek? Uvidíte vše v reálném čase!
Čas: 0 s
Uražená vzdálenost: 0 m
Pohyb nerovnoměrný
Představte si, že se rozjíždíte autem. Na rozdíl od rovnoměrného pohybu, kde se rychlost nemění, u nerovnoměrného pohybu se rychlost auta mění v čase. Pokud auto postupně nabírá rychlost, hovoříme o zrychleném pohybu, zatímco při brzdění jde o zpomalený pohyb.
Každodenní situace nám poskytují mnoho příkladů: auto se rozjíždí na semaforu, míč volně padající k zemi neustále zrychluje, zatímco vlak zpomaluje při příjezdu do stanice. Abychom takový pohyb mohli přesně popsat, rozlišujeme průměrnou a okamžitou rychlost. A pokud nás zajímá, jak se rychlost mění v čase, vstupuje do hry zrychlení.
Pohyb rovnoměrně zrychlený
Představte si auto, které se rozjíždí z klidu a každou sekundu svou rychlost pravidelně zvyšuje. Právě to je rovnoměrně zrychlený pohyb – pohyb, při kterém se rychlost tělesa rovnoměrně zvětšuje v závislosti na čase. Jinak řečeno přírustek rychlosti je konstantí v čase. Navíc platí že vektor zrychlení má stejný směr jako je vektor rychlosti tělesa.
Klíčovou veličinou je zrychlení, které zůstává konstantní a říká nám, jak moc se rychlost každou sekundu mění. Rovnoměrně zrychlený pohyb se dá matematicky popsat následovně:
Zrychlení je konstantní:
Rychlost \(v\) se mění lineárně s časem:
Dráha \(s\) roste kvadraticky v závislosti na čase:
\(s=v_{0}\times t + \frac{1}{2}\times a\times t^2\)
\(s\) je celkem uražená dráha \([\text{m}]\)
\(v_{0}\) je počáteční rychlost tělesa při které začelo těleso zrychlovat \([\text{m/s}]\)
\(a\) je konstantní zrychlení \([\text{m/s}^2]\)
\(t\) je uplynulý čas, po který jsme zkoumali pohyb tělesa \([\text{s}]\)
Tento vztah nám říká, že dráha roste kvadraticky s časem, což můžeme vidět i na grafu závislosti dráhy na čase – je to parabola.
Vizualizujte, jak se pohyb mění v čase!
- Graf rychlosti v čase je přímka se stoupající tendencí.
- Graf zrychlení v čase je vodorovná čára, protože zrychlení je konstantní.
- Graf dráhy v čase je parabola, což odráží skutečnost, že s časem roste dráha stále rychleji.
Následující vizualizace znázorňuje, jak se mění rychlost, zrychlení a uražená dráha při rovnoměrně zrychleném pohybu. Při spuštění animace se bod na všech třech grafech pohybuje současně, takže můžete v reálném čase sledovat, jak se mění jednotlivé veličiny.
Můžete si kdykoli animaci pozastavit nebo resetovat, abyste lépe pochopili jednotlivé fáze pohybu.
Kde se vzal kvadratický růst dráhy a proč je v jejím vzorci 1/2?
Představme si těleso, které se pohybuje rovnoměrně zrychleně. Co to znamená? Každou sekundu se jeho rychlost zvětší o stejnou hodnotu. Pokud například začneme z klidu a máme zrychlení 2 \(\text{m/s}^{2}\), pak za 1 sekundu se těleso pohybuje rychlostí 2 \(\text{m/s}\), za 2 sekundy se pohybuje rychlostí 4 \(\text{m/s}\), za 3 sekundy se už pohybuje rychlostí 6 \(\text{m/s}\) a tak dále…
Teď se zamysleme nad tím, jak velkou dráhu těleso urazí. Když se pohybovalo rovnoměrně (pořád stejnou rychlostí), stačilo vzít rychlost a vynásobit ji časem. Ale tady je háček – rychlost se postupně zvětšuje, takže těleso neurazí stejnou dráhu v každé sekundě!
Podívejme se na situaci detailněji:
- Na začátku pohybu je rychlost 0 \(\text{m/s}\), tedy se těleso ani nepohlo.
- Na konci první sekundy už je rychlost 2 \(\text{m/s}^{2}\). Průměrná rychlost za tuto sekundu je tedy (0 + 2) / 2 = 1 \(\text{m/s}\), což znamená, že urazilo 1 metr.
- Na konci druhé sekundy rychlost 4 \(\text{m/s}\). Průměrná rychlost mezi 1. a 2. sekundou je (2 + 4) / 2 = 3 \(\text{m/s}\), což znamená, že během této sekundy urazilo 3 metry.
- Podobně to pokračuje dál.
Vidíme tedy, že těleso urazí stále větší a větší vzdálenosti, což znamená, že dráha neroste lineárně, ale kvadraticky. Vzorec pro dráhu má tedy tvar:
\(s=v_{0} \times t+\frac{1}{2}a \times t^{2}\)
A kde se vzala ta \(\frac{1}{2}\)?
Při rovnoměrně zrychleném pohybu rychlost neroste skokově, ale postupně – každou sekundu se zvětší o stejnou hodnotu. To znamená, že během určitého časového intervalu není rychlost stále stejná, ale mění se od počáteční až po konečnou.
Když chceme spočítat dráhu, nemůžeme jednoduše vynásobit koncovou rychlost časem, protože po většinu pohybu bylo těleso pomalejší než na jeho konci. Místo toho musíme pracovat s průměrnou rychlostí za celý interval.
Aritmetický průměr dvou hodnot je dán vztahem:
\(v_{\text{průměr}} = \frac{v_0 + v_t}{2}\)
Pokud těleso na začátku stálo, tedy \( v_0 = 0 \), a jeho rychlost na konci intervalu byla \( v_t = a \times t \), pak průměrná rychlost vychází:
\( v_{\text{průměr}} = \frac{0 + a \times t}{2} = \frac{a \times t}{2} \)
Dráhu získáme jako součin průměrné rychlosti a času:
\( s = v_{\text{průměr}} \times t = \left(\frac{a \times t}{2} \right) \times t \)
Což po úpravě dává klasický vzorec pro dráhu rovnoměrně zrychleného pohybu:
\( s = \frac{1}{2} a t^2 \)
A kde se vzala část \( v_0 \times t \)? To odpovídá situaci, kdy těleso mělo už na začátku pohybu nějakou nenulovou rychlost. Pokud se už před zrychlováním pohybovalo rychlostí \( v_0 \), musíme přičíst i dráhu, kterou by urazilo bez jakéhokoliv zrychlení:
\( s = v_0 t + \frac{1}{2} a t^2 \)
Tento vzorec tedy vyjadřuje součet dráhy díky původní rychlosti a dráhy navíc způsobené zrychlením. Pokud bychom chtěli získat jen přírůstek dráhy způsobený zrychlením, jednoduše bychom část \( v_0 t \) odečetli.
Shrnutí:
Takže kdykoli vidíte \(s=v_{0}t + \frac{1}{2} a t^{2}\), vzpomeňte si na to, že jde o důsledek postupného růstu rychlosti a že průměrná rychlost v každém intervalu je průměrem mezi začátkem a koncem daného časového úseku.
Matematika tedy jen formálně zachycuje to, co už tušíme intuitivně – čím déle těleso zrychluje, tím větší vzdálenost urazí, a to nikoli rovnoměrně, ale stále rychleji!
Shrnutí
Pohyb rovnoměrně zpomalený
Představte si auto, které brzdí, aby zastavilo na značce stop a to je právě zpomalený pohyb. Rovnoměrně zpomalený pohyb je pohyb, při kterém se velikost rychlosti tělesa v čase rovnoměrně snižuje. To znamená, že jeho zrychlení \(a\) (přesněji zpomalení) je konstantní, ale na rozdíl od rovnoměrně zrychleného pohybu působí vektor zrychlení proti směru pohybu. Matematicky lze tento pohyb popsat dvěma způsoby v závislosti na volbě znaménka zrychlení \(a\):
1. Pokud považujeme zrychlení \(a\) za záporné (\(a<0\)), vzorce zůstávají stejné jako u rovnoměrně zrychleného pohybu, pouze hodnota zrychlení \(a\) je záporná:
Zrychlení je konstantní:
Rychlost \(v\) se mění lineárně s časem:
Dráha \(s\) kleasá kvadraticky v závislosti na čase:
\(s=v_{0} t + \frac{1}{2} a t^2\)
- V tomto případě hodnoty rychlosti \(v\) klesají, až nakonec dosáhnou nuly.
2. Pokud volíme zrychlení \(a\) (respektive o něm v tomto okamižku hovoříe jako o zpomalení) jako kladnou hodnotu (\(a>0\)), musíme musíme ve vzorcích pro rovnoměrně zrychlený pohyb upravit znaménko + na znaménko -, aby vzorce odpovídali zpomalování:
Zpomalení je konstantní:
Rychlost \(v\) se mění lineárně s časem:
Dráha \(s\) kleasá kvadraticky v závislosti na čase:
\(s=v_{0} t + \frac{1}{2} a t^2\)
- Tento přístup je často intuitivnější, protože přímo vyjadřuje, že rychlost klesá.
\(s\) je celkem uražená dráha [\(\text{m}\)]
\(v_{0}\) je počáteční rychlost tělesa při které začelo těleso zrychlovat [\(\text{m/s}\)]
\(a\) je konstantní zrychlení [\(\text{m/s}^{2}\)]
\(t\) je uplynulý čas, po který jsme zkoumali pohyb tělesa [\(\text{s}\)]
Jak vypadá rovnoměrně zrychlený pohyb graficky?
- Graf rychlosti v čase je přímka s klesající tendencí.
- Graf zpomalení v čase je vodorovná čára, protože zrychlení je konstantní.
- Graf dráhy v čase je obrácená parabola, což odráží skutečnost, že dráha nejprve rychle roste, ale růst se postupně zpomaluje, až se těleso zastaví.
Následující vizualizace znázorňuje, jak se mění rychlost, zrychlení a uražená dráha při rovnoměrně zrychleném pohybu. Při spuštění animace se bod na všech třech grafech pohybuje současně, takže můžete v reálném čase sledovat, jak se mění jednotlivé veličiny.
Můžete si kdykoli animaci pozastavit nebo resetovat, abyste lépe pochopili jednotlivé fáze pohybu.
Shrnutí:
Tento pohyb je běžnou součástí našeho života – auto brzdí před semaforem, míč hozený vzhůru zpomaluje pod vlivem gravitace, nebo cyklista přestane šlapat a postupně se zastaví kvůli odporu vzduchu a tření. Rovnoměrně zpomalený pohyb znamená, že rychlost tělesa se v každém časovém intervalu snižuje o stejnou hodnotu. Pokud například auto brzdí se zpomalením 2 \(\text{m/s}^{2}\), znamená to, že každou sekundu ztratí 2 \(m/s\) ze své rychlosti. Pokud tedy začínalo na rychlosti 10 m/s, za 5 sekund se úplně zastaví.
Tento pohyb lze popsat dvěma způsoby – buď jako zrychlení s negativní hodnotou, kdy se pužijí stejné vzorce jako v případě rovnoměrně zrychleného pohybu. Druhý přístup je v tom, že se v rovnicích pro rovnoměrně zrychlený pohyb nahradí znaménko + za znaménko – a počítá se v nich se zpomalením.
Volný pád
Volný pád je pohyb, při kterém na těleso působí pouze gravitace. Pokud bychom odstranili odpor vzduchu, všechna tělesa – ať už těžká kovová koule nebo lehké pírko – by padala se stejným zrychlením a dopadla by na zem ve stejný okamžik. To se dá krásně ověřit pokusem s Newtonovou trubicí, ve které odsajeme vzduch, čímž vytvoříme vakuum, a pozorujeme, že všechny objekty uvnitř trubice padají stejně. O vloném pádu se dá krásně řící, že je to pouze převlečený rovnoměrně zrychlený pohyb s nulovou počáteční rychlostí \(v_{0}\) a platí pro něj stejná pravidla.
Proč tomu tak je?
Důvodem je tíhové zrychlení, označované jako \(g\). To je přibližně 9,81 \(\text{m/s}^{2}\) (zaokrouhleně 10 \(\text{m/s}^{2}\)), tedy alepoň pro naše zeměpisné šířky (více se o tíhovém zrychlení dozvíte zde). Znamená to, že volně padající těleso získává každou sekundu rychlost o 9,81 \(\text{m/s}\) vyšší, tedy jeho rychlost roste rovnoměrně. Proto můžeme volný pád považovat za rovnoměrně zrychlený pohyb s konstantním zrychlením.
Gravitační zrychlení:
\( g = 9,81 \text{ m/s}^{2} \)
Okamžitá rychlost tělesa po čase \(t\) je dána vztahem:
\(v=gt\)
To znamená, že čím déle těleso padá, tím je rychlejší.
Uražená dráha \(s\) během volného pádu se vypočítá podobně jako u rovnoměrně zrychleného pohybu:
\(s=\frac{1}{2}gt^2\)
To ukazuje, že dráha roste kvadraticky – čím déle těleso padá, tím větší vzdálenost urazí.

\(s\) je celkem uražená dráha během volného pádu \([\text{m}]\)
\(g\) je konstantní tíhové zrychlení (9,81\(\text{ m/s}^{2}\)) \([\text{m/s}^{2}]\)
\(t\) je uplynulý čas, po který jsme zkoumali volný pád tělesa \([\text{s}]\)
Proč na Zemi vnímáme, že těžší předměty padají rychleji?
V běžném životě vidíme, že pírko padá pomaleji než kámen. To ale není způsobeno gravitací, nýbrž odporem vzduchu, který působí proti volnému pádu čímž ho zpoamluje. (Více o odporu vzduchu se můžete dozvědět zde) Pokud bychom odstranili vzduch, padaly by obě tělesa stejně rychle. Když se podíváte na měsíc, kde není atmosféra, můžete vidět astronauty, jak zkouší shodit kladivo a pírko současně – a obě dopadnou zároveň! Podobného jevu můžeme dosáhnout v Newtonově trubici, tedy trubici, ve které je vyčerpaný vzduch a je vní vytvořené vakuum.
Tíhové zrychlení jako případ klasického zrychlení:
Tíhové zrychlení \(\vec{g}\) je stále jen speciálním případem klasického zrychlení \(\vec{a}\) – je to vektorová veličina, což znamená, že má nejen velikost, ale i směr. V případě volného pádu směřuje vždy svisle dolů k zemi. Pokud se o něm bavíme bez šipky nad symbolem, obvykle tím myslíme pouze jeho velikost (9,81 m/s²), ale jeho skutečný význam je v tom, že určuje směr pohybu tělesa pod vlivem gravitace.
Rovnoměrný pohyb hmotného bodu po kružnici
Když sledujeme několik hmotných bodů pohybujících se po soustředných kružnicích (více kružnic, jenž mají střed ve stejném bodě), můžeme si všimnout zajímavé vlastnosti: všechny oběhnou kružnici za stejnou dobu, pokud mají stejnou úhlovou rychlost. To znamená, že jejich rotační pohyb vzhledem ke středu kružnice je stejný, ale jejich oblouková (dráhová) rychlost se může výrazně lišit. Podívejte se na následující animaci, která ilustruje tento problém.
Tento jev je důsledkem toho, že čím větší je poloměr kružnice, tím větší je dráha, kterou musí hmotný bod urazit, aby dokončilo jednu otáčku. Pokud se ale všechny hmotné body pohybují stejnou úhlovou rychlostí, pak ty, které jsou dále od středu, musí mít vyšší klasickou rychlost. Úhlovou rychlost si můžeme představit podobně jako klasickou rychlost, tentokrát to však není dráha za čas, ale úhlová rychlost je úhel za čas.
Úhlová rychlost – jak rychle se bod otáčí?
Při pohybu po kružnici místo obloukové (dráhové) rychlosti často používáme úhlovou rychlost \(\omega\), která udává, jak rychle se bod na kružnici otáčí. Úhlová rychlost stejně jako klasická rychlost je vektorová veličina. Definuje se jako velikost úhlu, kterou bod opíše za jednotku času:
\(\vec{\omega} = \frac{\Delta \vec{\varphi}}{\Delta t}\)
\(\vec{\omega}\) – vektor úhlové rychlosti [\(\text{rad/s}\)]
\(\Delta \vec{\varphi}\) – změna vektoru úhlu \([\text{rad}]\)
\(\Delta t\) – časový interval (změna času) \([\text{s}]\)
Co je to radián?
Radián je přirozená jednotka úhlu, která vychází přímo z geometrie kruhu. Zatímco stupně jsou založené na dělení kruhu na 360 částí, radiány vycházejí ze samotného vztahu mezi délkou oblouku a poloměrem kružnice.
Jak definujeme radián?
Jeden radián je takový úhel, při kterém délka oblouku odpovídá poloměru kružnice. To znamená:
\(s\) je délka oblouku \(\text{m}\)
\(r\) je poloměr kružnice \(\text{m}\)
Povšiměte si že dle předchozího vztahu je \(\text{rad}\) bezroměrná jednotka jelikož se nám v předchozím vztahu metry zkrátí a udavá tedy poměr mezi velikostí oblouku a jeho poloměrem.
Pokud by těleso opsalo celou kružnici, oblouk by měl délku obvodu kruhu, tedy:
Z definice radiánu pak vychází, že celý kruh odpovídá úhlu:
Tedy \(360°=2 \pi \text{ rad}\).

Vztah mezi stupni a radiány
Z předchozí rovnosti můžeme odvodit obecný převod mezi stupni a radiány:
\(1 \text{ rad} = \frac{180°}{\pi} \) a \(1° = \frac{\pi}{180} \text{ rad}\)
Což znamená, že můžeme převádět úhly následovně:
- \(90° = \frac{\pi}{2} \text{ rad}\)
- \(180° = \pi \text{ rad}\)
- \(270° = \frac{3 \pi}{2} \text{ rad}\)
- \(360° = 2 \pi \text{ rad}\)
Frekvence \(f\)udává, kolikrát se daný děj (např. otočení bodu po kružnici) zopakuje za jednu sekundu a měří se v hertzech (\(), kde \(\)1\text{ Hz} = 1 \text{ s}^{-1}\). Perioda \(T\) je doba potřebná k jednomu úplnému opakování děje a je s frekvencí v inverzním vztahu, tedy \(T=\frac{1}{f}\).
Pro celý oběh kružnice platí, že bod opíše úhel \(2\pi \text{ rad}\) jednu periodu \(T\):
\(\omega = \frac{2\pi}{T}\)
\(\omega\) – úhlová rychlost [\(\text{rad/s}\)]
\(T\) – perioda [\(\text{s}\)]
a souvisí s frekvencí otáček:
\(\omega = 2 \pi f\)
\(\omega\) – úhlová rychlost [\(\text{rad/s}\)]
\(f\) – frekvence \([\text{Hz}]\)
Úhlová rychlost je tedy stejná pro všechny hmotné body na soustředných kružnicích, pokud vykonávají otáčky synchronně.
Oblouková rychlost – závisí na poloměru
Zatímco úhlová rychlost všech těles na kružnicích se stejným středem, ale různým poloměrem, může být stejná, jejich oblouková (dráhová) rychlost \(v\) se liší, protože závisí na poloměru kružnice \(r\):
\(\vec{v} = \text{vec}(\vec{\omega},\vec{r})\)
Případně pokud nás zajímá pouze velikost dráhové rychlosti platí vztah:
\(v = \omega \times r\)
\(\vec{v}\) -dráhová rychlost \([\text{m/s}]\)
\(\vec{\omega}\) – úhlová rychlost \([\text{rad/s}]\)
\(\vec{r}\) – poloměr kružnice, po které se těleso pohybuje\([\text{m}]\)
To znamená:
- Hmotný bod na větší kružnici se pohybuje větší rychlostí, protože musí urazit delší dráhu za stejný čas.
- Hmotný bod blíže středu má nižší rychlost, protože jeho dráha je kratší.
Tento vztah potvrzuje, že úhlová rychlost určuje, jak rychle se těleso otáčí, zatímco oblouková (dráhová) rychlost říká, jak rychle se pohybuje po své kruhové dráze.
Poloha bodu na kružnici
Pro určení polohy bodu na kružnici používáme úhlovou dráhu \(\varphi\)
\(\varphi = \omega \times t \)
\(\omega\) – úhlová rychlost [\(\text{rad/s}\)]
\(\varphi\) – uražený úhel za čas \(t\) \([\text{rad}]\)
\(t\) – čas po které se těleso pohybovalo\([\text{s}]\)
Dostředivé zrychlení – proč se bod pohybuje po kružnici?
Ačkoliv velikost obloukové (dráhové) rychlosti zůstává stejná, její směr se neustále mění. To znamená, že existuje zrychlení, které udržuje těleso v kruhové dráze. Tomuto zrychlení říkáme dostředivé zrychlení \( a_d\) a směřuje vždy ke středu kružnice:
\(a_{d}=\frac{v^{2}}{r}=\omega^{2} \times r \)
\(a_{d}\) – dostředivé zrychlení \(t\) \([\text{m/s}^{2}]\)
\(\omega\) – úhlová rychlost [\(\text{rad/s}\)]
\(v\) – dráhová rychlost [\(\text{m/s}\)]
\(r\) – poloměr kružnice, po které se hmotný bod pohybuje \([\text{m}]\)

Bez tohoto zrychlení by těleso pokračovalo přímočaře, ale protože na něj působí síla směrem do středu (např. gravitace u planet nebo tření u pneumatik auta), zůstává na kruhové dráze.
Shrnutí:
Při pohybu hmotného bodu po kružnici platí několik důležitých pravidel. Úhlová rychlost je stejná pro všechna tělesa, která rotují kolem stejného středu se stejnou frekvencí, což znamená, že všechny body oběhnou kružnici za stejný čas bez ohledu na svou vzdálenost od středu. Oblouková (dráhová) rychlost \(v\) (tedy rychlost měřená v metrech za sekundu) však závisí na poloměru kružnice – čím je bod dále od středu, tím větší vzdálenost urazí za stejný čas, a tedy se pohybuje rychleji. Poloha bodu na kružnici se určuje pomocí úhlu \(\varphi = \omega \times t \), kde \(\omega\) je úhlová rychlost a \(t\) je čas. Tento vztah nám umožňuje popsat, kde se bod nachází v libovolném okamžiku. Aby těleso zůstalo na kruhové dráze, působí na něj dostředivé zrychlení \(a_{d}\), které ho neustále směruje ke středu kružnice a zabraňuje mu v tom, aby se pohybovalo přímočaře.
Závěr
Kinematika je základní oblast fyziky, která se zabývá popisem pohybu těles bez ohledu na síly, které jej způsobují. Při studiu pohybu jsme si představili hmotný bod, což je ideální model tělesa, který nám umožňuje jednodušší analýzu různých typů pohybu. Prozkoumali jsme rovnoměrný i nerovnoměrný pohyb, přímý i křivočarý pohyb, a také jsme si ukázali rozdíl mezi rychlostí a zrychlením, včetně jejich vektorové povahy.
Ve zvláštním případě rovnoměrného pohybu po kružnici jsme si vysvětlili význam úhlové rychlosti a vztah mezi ní a klasickou dráhovou rychlostí. Ukázali jsme si také, že pohyb po kružnici je možný pouze díky dostředivému zrychlení, které těleso neustále stáčí směrem ke středu.
Nyní si zopakujeme klíčové fyzikální veličiny a pojmy z obalasit kinematiky.
Důležité definice:
Kinematika – Fyzikální disciplína, která studuje pohyb těles bez ohledu na síly, které jej způsobují. Zaměřuje se na veličiny jako dráha, rychlost a zrychlení.
Hmotný bod – Model tělesa, jehož rozměry zanedbáváme, protože jsou vzhledem k dané situaci nepodstatné. Používá se ke zjednodušení popisu pohybu.
Trajektorie – Geometrická čára, po které se těleso při svém pohybu pohybuje. Může být přímá nebo zakřivená.
Dráha – Délka trajektorie, kterou těleso urazí za určitou dobu. Udává se v metrech.
Rychlost – Vektorová veličina vyjadřující změnu polohy tělesa za jednotku času. Její jednotkou je metr za sekundu.
Zrychlení – Vektorová veličina udávající změnu rychlosti v čase. Pokud se rychlost zvětšuje, mluvíme o zrychlení, pokud se zmenšuje, mluvíme o zpomalení.
Pohyb rovnoměrný – Pohyb, při kterém těleso urazí za stejné časové úseky stejnou dráhu. Rychlost je konstantní.
Pohyb nerovnoměrný – Pohyb, při kterém se rychlost tělesa v čase mění. Může být zrychlený nebo zpomalený.
Pohyb přímočarý – Pohyb, při kterém je trajektorií přímka.
Pohyb křivočarý – Pohyb, při kterém trajektorie není přímka, ale nějaká křivka (například parabola nebo kružnice).
Posuvný pohyb – Pohyb, při kterém všechny body tělesa opisují stejnou trajektorii a za stejný čas urazí stejnou dráhu. Příkladem je pohyb auta po silnici nebo výtahu nahoru a dolů.
Pohyb tělesa po kružnici – Pohyb tělesa, při kterém se těleso pohybuje kolem pevného bodu po kruhové trajektorii. Charakterizuje jej úhlová a obvodová rychlost a dostředivé zrychlení.